Standardabweichung – das Wichtigste vorweg
- In der Optionspreisgestaltung wird die Standardabweichung als Maß für die Volatilität eines zugrunde liegenden Wertes verwendet. Volatilität ist ein wichtiger Faktor bei der Bestimmung des Optionspreises; je höher die Volatilität, desto wertvoller ist die Option.
- Die Standardabweichung ist ein integraler Bestandteil des Black-Scholes-Modells zur Optionspreisgestaltung. In diesem Modell steht die Standardabweichung für die erwartete Schwankung des Basiswertes über die Laufzeit der Option.
- Die historische Volatilität, die aus historischen Preisänderungen des Basiswertes berechnet wird, ist oft ein Indikator für die zukünftige Volatilität, jedoch nicht immer perfekt. Die implizite Volatilität, die aus den aktuellen Optionspreisen abgeleitet wird, berücksichtigt die Erwartungen des Marktes hinsichtlich zukünftiger Preisbewegungen und damit auch der Standardabweichung.
- Da die Standardabweichung die erwartete Schwankung des Basiswertes widerspiegelt, hat sie einen direkten Einfluss auf den Optionspreis. Ein Anstieg der Standardabweichung (und damit der Volatilität) führt zu einem Anstieg der Optionspreise.
- Die Kenntnis der Standardabweichung kann auch dabei helfen, das Risiko bei der Optionsstrategie zu managen. Ein Trader kann beispielsweise Optionen mit einer höheren Standardabweichung kaufen, wenn er glaubt, dass der Markt volatil sein wird, oder Optionen mit einer geringeren Standardabweichung verkaufen, wenn er glaubt, dass der Markt stabil bleiben wird.
Wenn wir Optionen handeln, bedienen wir uns mathematischer und statistischer Kenngrößen. Der Kern des Stillhaltergeschäfts ist es, die Wahrscheinlichkeit auf unserer Seite zu haben. Große Beachtung finden dabei die Kursmarken der Standardabweichung.
Aus der Schulzeit mag an dieser Stelle die Glockenkurve von Carl Friedrich Gauß in Erinnerung treten. Die Verbindung zum Optionshandel möchte ich in diesem Artikel gerne vereinfacht darstellen.
Die Standardabweichung für den Optionshandel nutzen
Grundlagen aus der Statistik
Ausgehend von der statistischen Mathematik finden sich in einer Menge bestimmte Sachverhalte in unterschiedlicher Anzahl oder Ausprägung. Überwiegend wird als Beispiel die Körpergröße von Menschen herangezogen. So lässt sich ein Durchschnitt ermitteln, der als Erwartungswert bezeichnet wird.
Die Normalverteilung beschreibt dann die Abweichung vom Durchschnitt in Umfang und Ausprägung. Diese Streuung folgt in unterschiedlichsten Themen und Betrachtungsbereichen einem wiederkehrenden Schema.
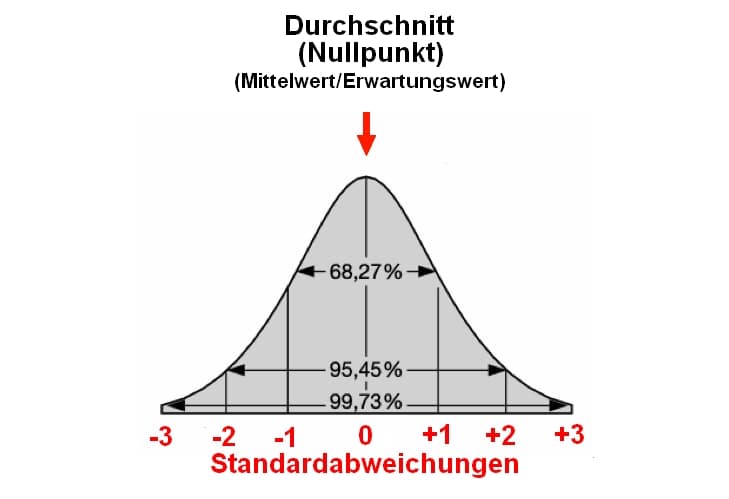
Aus der Varianz der erhobenen Daten lässt sich die Standardabweichung berechnen. Innerhalb einer Standardabweichung vom Mittelwert nach oben und einer nach unten befinden sich dann 68,27 % der Datensätze. Häufig werden die Datensätze auch als Fallzahlen, Vorgänge, etc. bezeichnet.
Im nächsten Bereich der Glockenkurve wird eine weitere Standardabweichung nach oben und unten hinzugefügt. Dieser Abschnitt beinhaltet dann 95,45 % der Fälle.
Folglich ergibt sich mit hinzufügen der letzten Standardabweichung eine weitere Eingrenzung der Fälle. Damit lassen sich innerhalb von drei Standardabweichungen plus und minus vom Erwartungswert 99,73 % aller Vorgänge finden.
Kostenloses E-Book
Endlich Chartmuster verstehen & dein Trading verbessern
Mit diesen Gratis-Tipps wirst Du lernen:
10 Chartmuster für eine effektivere Chartanalyse
Auf welchen Trend diese Muster zukünftig deuten
Wie Du dadurch gute Trade-Einstiege findest

Kostenloses E-Book
Hole Dir jetzt die Tipps, um Chartmuster zu verstehen & dein Trading zu verbessern
10 Chartmuster für eine effektivere Chartanalyse
Auf welchen Trend diese Muster zukünftig deuten
Wie Du dadurch gute Trade-Einstiege findest

Kostenloses E-Book
Hole Dir jetzt die Profi-Tipps für Chartmuster und verbessere Dein Trading

Graphische Darstellung der Normalverteilung
Veranschaulichen lässt sich das durch die folgende Grafik:
Diese nahezu einhundert prozentige Wahrscheinlichkeit kann den Optionshändler schon fast in Euphorie versetzen. Um die Hoffnung gar nicht erst ins unermessliche wachsen zu lassen, muss ich das an dieser Stelle ins Verhältnis setzen:
Die theoretische Wahrscheinlichkeit kann trügen
Auch in den verbleibenden 0,27 % Wahrscheinlichkeit steckt genug Potenzial für ein sogenanntes Black Swan Event. Die Werte, die sich in diesem Bereich wiederfinden, können jede Erwartung sprengen.
Darüber hinaus ergeben sich außerhalb der ersten Standardabweichung nur selten attraktive Prämien für Stillhaltergeschäfte.
Wie so oft an der Börse können wir aus Daten der Vergangenheit die schönsten Szenarien bauen. Und genau in dieser Vergangenheit finden wir dann auch Hinweise, dass es manchmal genau anders kommen kann.
Auf den mathematischen Hintergrund möchte ich an dieser Stelle nicht weiter eingehen. Die Formeln und Herleitung der Thematik ist unter diesen Links sehr anschaulich erläutert:
Die Anwendung im Optionshandel
Die Kursbewegungen eines Basiswerts lassen sich ebenfalls statistisch festhalten. Sinnvoll wäre zum Beispiel das Dokumentieren der Handelsspanne eines Tages. Ebenso könnte der Unterschied der Tages- Wochen- oder Monatsschlusskurse eine validierbare Datenmenge ergeben.
Da sich die Stärke von Kursschwankungen auf die Preise der Optionen auswirkt, untersuchen wir zuerst die historische Volatilität. Genau diese wird auf Basis der Schlusskurse für die letzten 30 Tage ermittelt und in Prozent angegeben. Hierbei ist irrelevant, ob der Kurs im Vergleich zum Vortag gestiegen oder gefallen ist.
Also wenn eine Aktie täglich um 1,5 Prozent fällt ist die Historische Volatilität (abgekürzt “HV”) ebenso, als würde sie an einem Tag um 1,5 Prozent steigen und am nächsten wieder um 1,5 Prozent fallen. Genauso kann eine Aktie mit einer HV von 0,4 Prozent plötzlich an einem Tag um 10 Prozent schwanken.
Wie sich die HV in der Handelssoftware TWS von CapTrader darstellen lässt, zeigt dieser Screenshot:
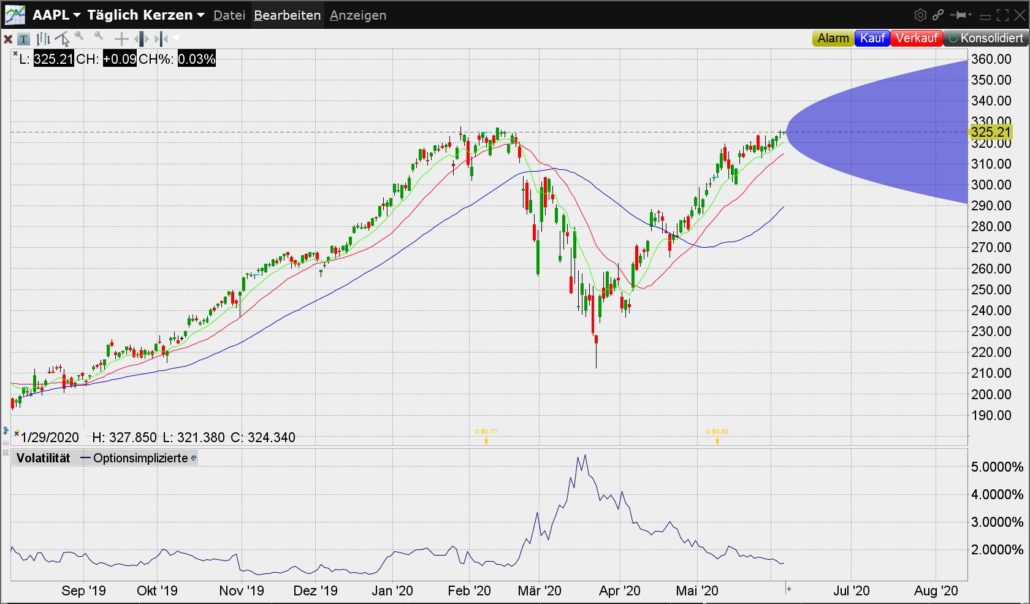
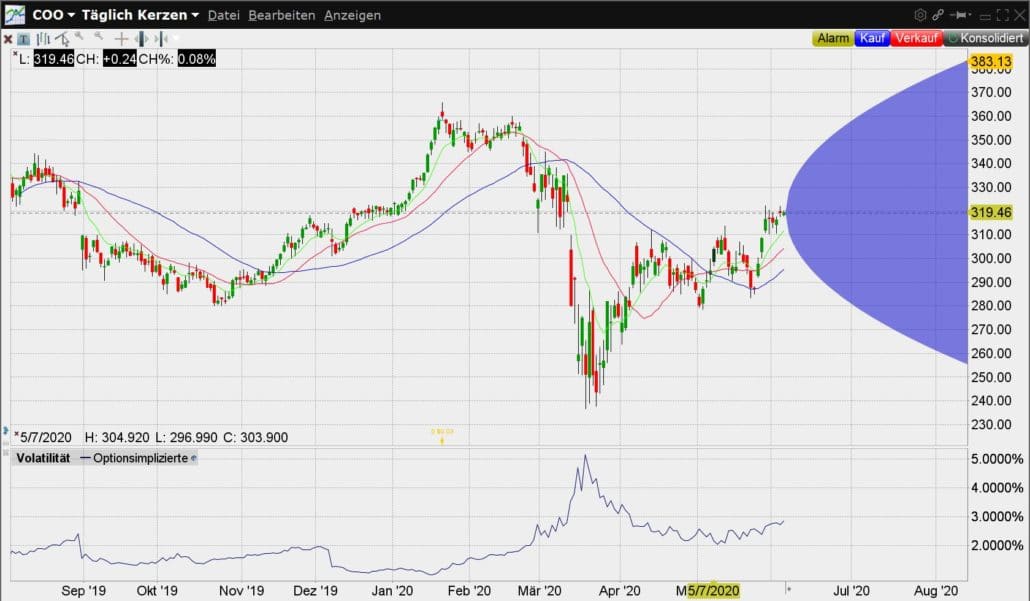
Für das folgende Beispiel habe ich bewusst zwei Aktien herausgesucht, die auf den ersten Blick vergleichbare Parameter haben. Der Kurs liegt jeweils nahe an 320 US-Dollar. Zudem liegt die historische Volatilität um 1,8 Prozent. Auch ist die HV zum Schlusskurs des Vortags nahezu gleich.
Davon ausgehend lässt sich annehmen, dass der Kursverlauf aus der Vergangenheit sich ebenfalls ähnelt. Für einen Vergleich habe ich die Charts einmal untereinander platziert:
Der Unterschied von lediglich 0,025 % in der historischen Volatilität drückt sich im Chart meiner Meinung nach stärker aus als erwartet. Die Gaps und einzelne lange Kerzen fallen bei Cooper größer aus als bei Apple. Dadurch, dass die Abstände der Schlusskurse relevant sind, bleiben die Auswirkungen auf die Berechnung der HV gering.
Aber nun fällt doch eine starke eine Besonderheit ins Auge. Wir finden eine Art Glockenkurve wieder. Und diese unterscheiden sich deutlich in ihrer Ausprägung. Während sich bei Apple am Ende des Charts circa 70 Dollar Spanne bilden, sind es bei Cooper schon 130.
Woher kommt nun dieser Unterschied, wenn doch die anderen Kennzahlen annähernd identisch sind? Das Geheimnis liegt in der impliziten Volatilität. Im Screenshot aus der TWS habe ich die einmal rot umrandet.
Ein deutlicher Unterschied
Hier stehen 1,5 % von Apple einem Wert von 2,85 % bei Coopers gegenüber. Das ist fast das Doppelte oder, um genau zu sein, das 1,9-Fache. Nun setzen wir die grob geschätzten Dollar-Spannen der Glockenkurven aus den Charts in Verhältnis und kommen auf 1,86. Das ist auch kein Zufall. Die Kurve spiegelt eine angenommene Standardabweichung für die Zukunft wieder.
Das bedeutet, der Kurs des Basiswerts wird mit einer Wahrscheinlichkeit von 68,27 % im Bereich der graphisch dargestellten Glocke verlaufen. Im Gegenzug kann er sich natürlich zu 31,73 auch außerhalb dieses Bereichs wiederfinden.
Die Glocke als Glaskugel?
Die implizite Volatilität ergibt sich aus den Preisen der Optionen für das Underlying. Die Preise werden am Markt durch Angebot und Nachfrage bestimmt. Eine Nachfrage entsteht durch das Bedürfnis der Marktteilnehmer, von Kursbewegungen zu profitieren und/oder bestehende Positionen absichern zu wollen.
Entsprechend lässt sich behaupten, dass die Volatilität ein Maß für Unsicherheit darstellt. Diese kann durch Nachrichten zum Unternehmen hervorgerufen werden. Ebenso steigt die Unsicherheit im Markt bei bevorstehenden Ereignissen mit ungewissem Ausgang.
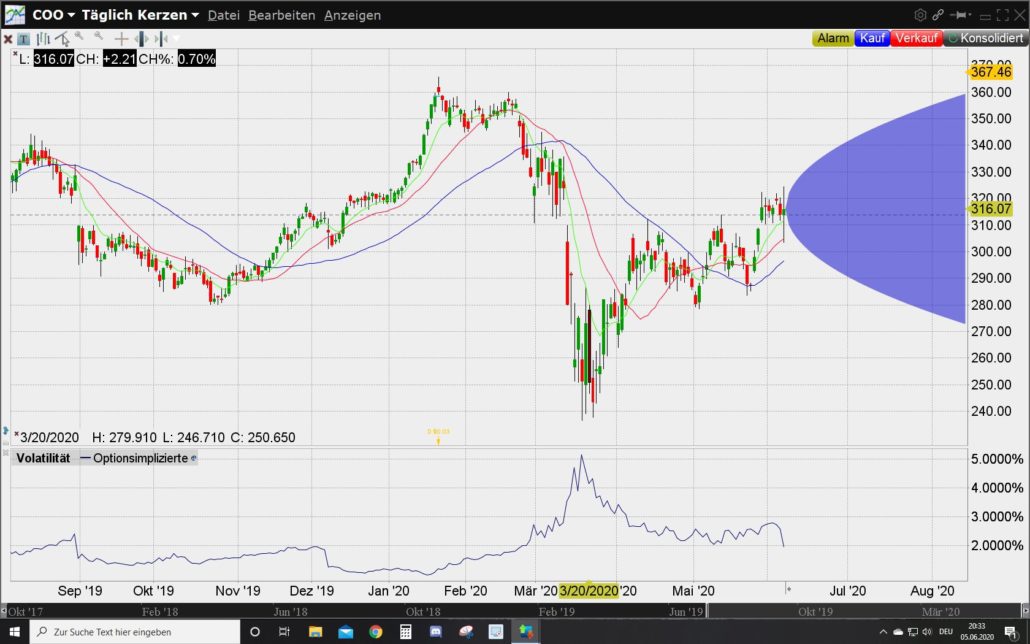
Bei Aktien ist der Termin für den Quartalsbericht ein gutes Beispiel. Der Screenshot von Cooper entstand vor der Veröffentlichung der Quartalszahlen. Mit der Betrachtung des Charts am Tag danach lässt sich gut erkennen, wie mit der gewichenen Unsicherheit über das Ergebnis auch die implizite Volatilität gesunken ist:
Die Vergangenheit übernimmt keine Garantie für die Zukunft
Damit ist sicher, dass die Prognose der zukünftigen Kursentwicklung immer eine Momentaufnahme der aktuellen Situation darstellt. An der Börse werden überwiegend Erwartungen gehandelt. Wenn die Fakten den Erwartungen nicht folgen können, werden daraus Enttäuschungen. Zumindest Ernüchterung in Form von Konsolidierung.
Kostenloses E-Book
10 technische Indikatoren für Deinen Trading-Erfolg!
Sichere Dir jetzt die Gratis-Tipps und Du wirst lernen:
Wie Du profitabler durch Indikatoren wirst
Welche Vorteile Indikatoren bieten
Wann Du welche Indiktoren richtig anwendest

Kostenloses E-Book
10 technische Indikatoren für Deinen Trading-Erfolg! Du wirst lernen:
Wie Du profitabler durch Indikatoren wirst
Welche Vorteile Indikatoren bieten
Wann Du welche Indiktoren richtig anwendest

Kostenloses E-Book
Hole Dir jetzt 10 technische Indikatoren für Deinen Trading-Erfolg!

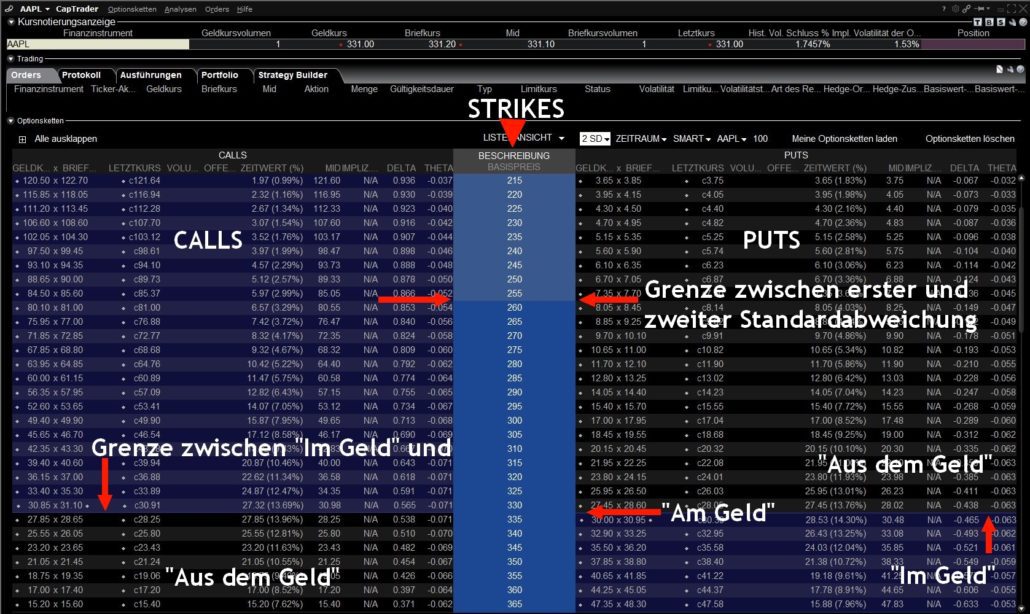
Darstellung der Standardabweichung in der Optionskette
In der Option Chain der Brokersoftware werden die Standardabweichungen ebenfalls dargestellt. Ergänzend zu den Marken aus dem Chart lässt sich dann einfach ein passender Strike für die aktuelle Handelsidee finden.
Fazit zur Standardabweichung
Die Standardabweichung umfasst Kursbereiche, an denen sich die Marktteilnehmer aufgrund statistischer Wahrscheinlichkeiten orientieren können. Im Optionshandel dient sie uns, die Strikes für entsprechende Handelsideen zu finden. Darüber hinaus lassen sich die Strikes in Relation zur erwarteten Kursbewegung setzen.
FAQ zur Standardabweichung
Was ist die Standardabweichung im Optionshandel?
Die Standardabweichung ist ein statistisches Maß, das die erwartete Schwankung oder Volatilität eines zugrunde liegenden Wertes (wie einer Aktie) darstellt. Sie spielt eine wichtige Rolle bei der Preisgestaltung und dem Handel von Optionen.
Was misst die Standardabweichung?
In Bezug auf die Basispreise der Optionen lässt sich die Wahrscheinlichkeit möglicher Kursbewegungen im Basiswert abschätzen. Abhängig von der impliziten Volatilität wird für die erste Standardabweichung eine Preisspanne ermittelt, in der sich der Kurs am Verfallstag mit einer Wahrscheinlich von 68,27% befinden kann.
Ist Standardabweichung gleich Volatilität?
Nein. Die Volatilität wirkt sich auf die Breite der Standardabweichung aus, sodass sich mit höherer Volatilität auch die Kursspanne erhöht, die als Standardabweichung definiert wird.
Wie lässt sich die Standardabweichung darstellen?
In der Regel werden die Standardabweichungen in der Optionskette der Handelssoftware optisch dargestellt. In der Trader Workstation ist auch die Darstellung im Chart möglich. Wo die Einstellung dafür zu finden ist, wird im Artikel gezeigt: Die Glocke als Glaskugel
Wie wird die Standardabweichung im Black-Scholes-Modell verwendet?
Im Black-Scholes-Modell zur Optionspreisgestaltung steht die Standardabweichung für die erwartete Schwankung des Basiswertes über die Laufzeit der Option. Ein Anstieg der Standardabweichung würde zu einem Anstieg des Optionspreises führen.
Was ist der Unterschied zwischen historischer und impliziter Volatilität?
Die historische Volatilität bezieht sich auf die tatsächlichen Preisbewegungen des Basiswerts in der Vergangenheit und wird oft zur Berechnung der Standardabweichung verwendet. Die implizite Volatilität hingegen wird aus den aktuellen Optionspreisen abgeleitet und repräsentiert die erwartete zukünftige Schwankung des Basiswerts.
Wie beeinflusst die Standardabweichung den Preis einer Option?
Die Standardabweichung beeinflusst den Optionspreis, indem sie als Maß für die Volatilität des Basiswertes dient. Je größer die erwartete Schwankung (und damit die Standardabweichung), desto größer ist das Risiko und desto höher ist der Optionspreis.
Wie kann die Standardabweichung beim Risikomanagement helfen?
Durch das Verständnis der Standardabweichung und deren Auswirkungen auf den Optionspreis können Händler besser beurteilen, welches Risiko sie eingehen möchten. Beispielsweise könnten sie Optionen mit einer höheren Standardabweichung kaufen, wenn sie glauben, dass der Markt volatil sein wird, oder Optionen mit einer niedrigeren Standardabweichung verkaufen, wenn sie glauben, dass der Markt stabil bleiben wird.
Ist eine höhere Standardabweichung immer besser?
Nicht unbedingt. Eine höhere Standardabweichung bedeutet eine größere erwartete Schwankung und damit ein höheres Risiko. Ob das gut oder schlecht ist, hängt von der spezifischen Marktsituation und der Risikotoleranz des Händlers ab. Einige Händler könnten eine höhere Volatilität als Chance für größere Gewinne sehen, während andere sie als zu riskant betrachten könnten.
Weiterlesen – Die Artikelreihe „Optionen handeln“
Folgende Teile dieser Serie sind bereits erschienen:
- #01 – Optionen handeln – Der erfolgreiche Einstieg
- #02 – Der Long Call
- #03 – Der Long Put
- #04 – Der Short Call
- #05 – Der Short Put
- #06 – Die Standardabweichung
- #07 – Implizite Volatilität und das IVR
- #08 – Optionsuniversum – Vorstellung der GuV Software
- #09 – Jens Rabe – Portrait des Optionshändlers
- #10 – Tastytrade – Der US-Broker für Optionen, Aktien, Futures
- #11 – Optionsstrategien
- #12 – Trader Workstation (TWS) – Optionen handeln
Sie sind gerne eingeladen, mir im weiteren Verlauf zu folgen. Ich freue mich darauf, das Thema mit Ihren Fragen, Anregungen und konstruktiver Kritik dynamisch gestalten zu können.